什么是Normalization?
Normalization:规范化或标准化,就是把输入数据X,在输送给神经元之前先对其进行平移和伸缩变换,将X的分布规范化成在固定区间范围的标准分布。 $$ h = f(g \cdot \frac{x - \mu}{\sigma} + b) $$ 其中 $\mu$ 为均值,$\sigma$ 为方差,$g$ 为缩放参数,$b$ 为平移参数。归一化得到的数据符合均值为 $b$ 、方差为 $g^2$ 的分布。
Batch Norm
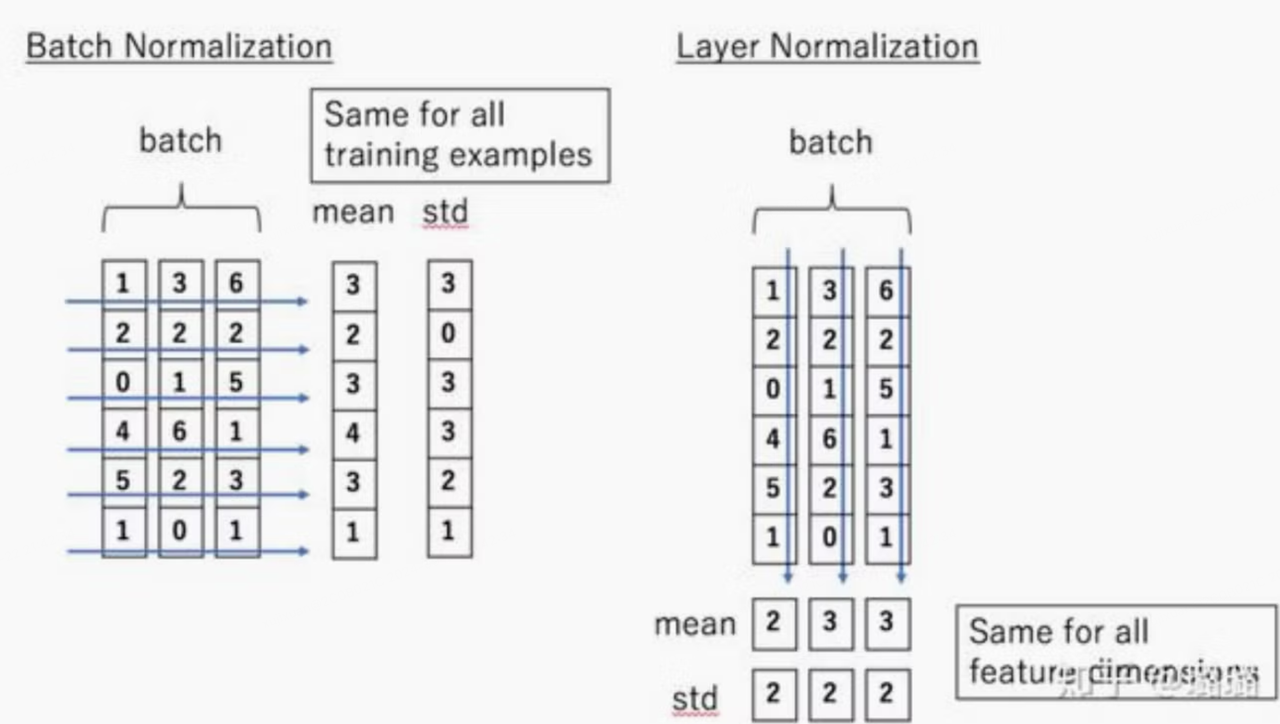
Batch Norma 的处理对象是对一批样本,对batch size这一维度做reduce,是对这一batch下样本的同一维度特征做归一化。
计算公式为: 均值: $$ \mu_B = \frac{1}{m} \sum_{i=1}^{m} x_i $$ 其中,m 是当前 batch 中样本的数量,$\mu_B$ 是输入的均值。
方差: $$ \sigma^2_B = \frac{1}{m} \sum_{i=1}^{m} (x_i - \mu_B)^2 $$ 归一化: $$ \hat{x}_i = \frac{x_i - \mu_B}{\sqrt{\sigma^2_B + \epsilon}} $$ 缩放平移: $$ y_i = \gamma \hat{x}_i + \beta $$
Layer Norm
Layer Norm 的处理对象是是单个样本,对hidden size维度做reduce,是对这单个样本的所有维度特征做归一化。
BN、LN可以看作横向和纵向的区别。经过归一化再输入激活函数,得到的值大部分会落入非线性函数的线性区,导数远离导数饱和区,避免了梯度消失,这样来加速训练收敛过程。BatchNorm这类归一化技术,目的就是让每一层的分布稳定下来,让后面的层可以在前面层的基础上安心学习知识。BatchNorm就是通过对batch size这个维度归一化来让分布稳定下来。LayerNorm则是通过对Hidden size这个维度归一。
RMS Norm
Recall:BatchNorm公式为,元素减均值除方差后,乘gama的缩放参数,再加beta的shift参数。layerNorm与BatchNorm公式类似,都是计算均值和方差后,对归一化后的元素进行缩放和平移。
RMS Norm是简化版本的layerNorm,RMSNorm移除了LayerNorm中的均值项(由于没有计算均值,所以方差计算也没有了减去均值的操作)。
计算公式为: $$ \bar{a_i}=\frac{a_i}{RMS(a)}g_i, \quad \text{where } RMS(a)=\sqrt{\frac{1}{n}\sum_{i=1}^{n}a_i^2}. $$
从公式中可以看出,RMSNorm移除了LayerNorm中的均值项(由于没有计算均值,所以方差计算也没有了减去均值的操作)。
总的来说,RMSNorm是对LayerNorm的一种简化,它的计算效率更高。并且原论文的实验结果显示这种简化并没有对模型的训练速度和性能产生明显影响。